【学习笔记】CS224W速记(图模型专题)
时间:2022-10-22 20:30:00
序言
本文针对2021年秋季CS224W课程slides速记,没有作业答案。
CS224W事实上,它更倾向于研究理论计算机方向(如图论),而不是关注图形神经网络,所以许多内容非常理论,本文是作者花两天时间记录一些有用的点,更倾向于图形神经网络应用摘要,一些不理解部分暂时没有深入讨论,只是留下一个印象。
课程链接:http://web.stanford.edu/class/cs224w/
文章目录
- 序言
-
- 节点中心度
- 图基元
- 计算两个节点之间路径总数的巧解
- 图核
- 随机游走节点嵌入
- 整图嵌入
- PageRank算法
- 二分图推荐
- 传递节点分类的消息
- 替换等变异性
- GCN(mean-pool)
- 新闻计算与新闻聚合
- GraphSage(max-pool)
- GAT
- GNN使用技巧
- GIN
- 异构图
- RGCN
- 知识表示学习
- 知识图谱和多级推理
- 子图与Motif
- 神经子图匹配(不懂)
- 推荐系统
- Louvain算法
- GraphRNN
- 一些前沿研究
- LightGCN概述
节点中心度
给定无向图 G = ( V , E ) G=(V,E) G=(V,E),节点 v v v的中心度(centrality) c v c_v cv用于测量节点 v v v具体有以下计算方法:
-
特征向量中心度(eigenvector centrality):节点的重要性取决于相邻节点的重要性
c v = 1 λ ∑ u ∈ N ( v ) c u ∈ R c_v=\frac1\lambda\sum_{u\in N(v)}c_u\in\R cv=λ1u∈N(v)∑cu∈R
其中 N ( v ) N(v) N(v)表示节点 v v v的邻接点, λ > 0 \lambda>0 λ>0为标准化系数。求解上式等价于求解 λ c = A c \lambda{\bf c}=A{\bf c} λc=Ac,其中 A A A为无向图 G G G的邻接矩阵,因此等价于求解 A A A的特征值与特征向量,根据Perron-Fronbenius定理可知, λ max \lambda_{\max} λmax必然为正,则通常使用最大特征值 λ max \lambda_{\max} λmax对应的特征向量 c max {\bf c}_{\max} cmax作为式 ( 1 ) (1) (1)的解。
-
中介中心度(betweenness centrality):节点重要性由它中转多少对节点之间的最短路径决定
c v = ∑ s ≠ v ≠ t count(shortest paths between s and t that contain v ) count(shortest paths between s and t ) (2) c_v=\sum_{s\neq v\neq t}\frac{\text{count(shortest paths between } s\text{ and }t\text{ that contain }v)}{\text{count(shortest paths between } s\text{ and }t)}\tag{2} cv=s=v=t∑count(shortest paths between s and t)count(shortest paths between s and t that contain v)(2)
如在无向图 ( A , C ) , ( B , C ) , ( C , D ) , ( B , D ) , ( D , E ) (A,C),(B,C),(C,D),(B,D),(D,E) (A,C),(B,C),(C,D),(B,D),(D,E)中, c A = c B = c E = 0 , c C = c D = 3 c_A=c_B=c_E=0,c_C=c_D=3 cA=cB=cE=0,cC=cD=3 -
紧密中心度(closeness centrality):节点重要性由它与所有其他节点的距离之和决定
c v = 1 ∑ u ≠ v shortest path length between u and v c_v=\frac1{\sum_{u\neq v}\text{shortest path length between } u\text{ and }v} cv=∑u=vshortest path length between u and v1
如在无向图 ( A , C ) , ( B , C ) , ( C , D ) , ( B , D ) , ( D , E ) (A,C),(B,C),(C,D),(B,D),(D,E) (A,C),(B,C),(C,D),(B,D),(D,E)中, c A = 1 / 8 , c D = 1 / 5 c_A=1/8,c_D=1/5 cA=1/8,cD=1/5
图基元
-
首先定义图的同形(isomorphism):称两个节点数相等的图 G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1)与 G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2)是同形的,若存在一一映射 f : V 1 → V 2 f:V_1\rightarrow V_2 f:V1→V2,使得 E 1 = E 2 E_1=E_2 E1=E2(比如五角星和五边形就是同形图)。
判断两个图是否同形是NP-hard
-
图基元(graphlets):非同形的图构成的集合。
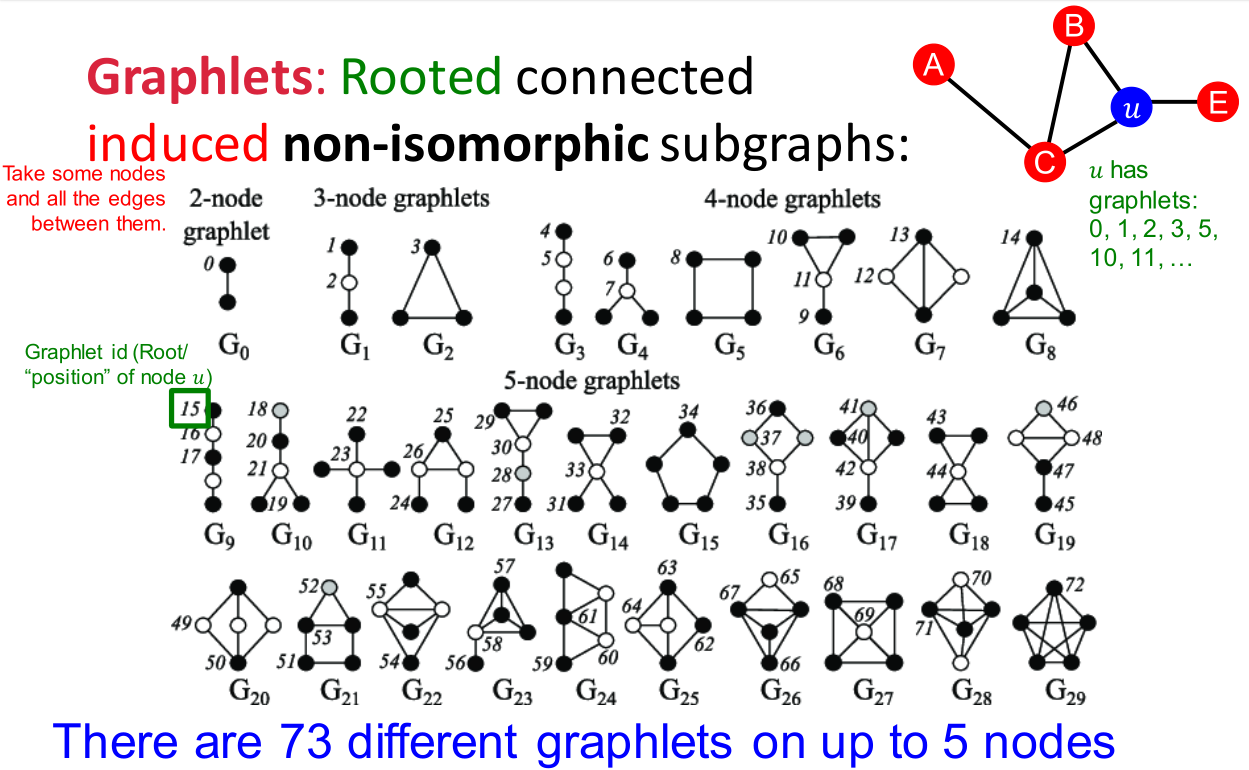
比如上图中陈列节点数不超过 5 5 5的所有图基元,节点上标号记录不同类型的图基元节点(如 G 8 G_8 G8中的 4 4 4个节点本质上是同类)。
节点数 图基元数量 累积不同图基元节点数量 2 2 2 1 1 1 1 1 1 3 3 3 2 2 2 4 4 4 4 4 4 6 6 6 15 15 15 5 5 5 21 21 21 73 73 73 事实上图基元未必一定是连通图,但是上图和上表中统计的都是连通情况下的计数。
-
图基元度向量(graphlet degree vectors,GDV):
节点 u u u的GDV由它所在的子图中不同图基元节点出现频率构成。
如上图所示,只考察节点数不超过 3 3 3的图基元,共计 4 4 4种不同的图基元节点 a , b , c , d a,b,c,d a,b,c,d,考察节点 u u u分别作为这四类节点出现的次数,得到的GDV为 [ 2 , 1 , 0 , 2 ] [2,1,0,2] [2,1,0,2]
计算两个节点之间路径总数的巧解
定义无向图 G = ( U , V ) G=(U,V) G=(U,V)邻接矩阵 A A A:
A u v = { 1 if u ∈ N ( v ) 0 if u ∉ N ( v ) A_{uv}=\left\{\begin{aligned} &1&&\text{if }u\in N(v)\\ &0&&\text{if }u\notin N(v) \end{aligned}\right. Auv={
10if u∈N(v)if u∈/N(v)
定义路径计数矩阵 P ( n ) P^{(n)} P(n):
P u v ( n ) = count(paths of length n between u and v ) P^{(n)}_{uv}=\text{count(paths of length }n\text{ between} u\text{ and }v) Puv(n)=count(paths of length n betweenu and v)
则可以证明 P ( n ) = A n P^{(n)}=A^n P(n)=An,这里的路径可以不是简单路径(即路径重可以存在环或重复边)。
可以通过数学归纳法证明:
P u v ( n



