数据处理之小波分析

分析信号时频域

在傅里叶变换中，信号可以用三角函数展开，而在小波变换中，信号可以用小波基展开。与三角函数相比，小波基是能量集中有限的信号。

傅里叶展开式：
$$f(t)=a_0\sum _{n=1}^{\infty }(a_{n}cosn{w}_{0}t{b}_{n}sinn{w}_{0}t)$$
小波基展开式：
$$f(t)=\sum _{k\in Z}{c}_k\phi (2^{j}t-k)$$
j起到缩放函数的作用类似傅里叶中w，k是平移因子

由于平移因子的作用，小波变换可以对局部细节进行分析，并且窗口大小是变化的。而傅里叶变换针对整个函数（周期）进行分析。

小波变换分解表达式：
$$f(t)=\sum _{j=1}^{\infty }\sum _{k\in Z}{c}_{j,k}\psi (2^{j-1}(t-k))+\sum _{k\in Z}{d}_k\phi (t-k)$$

$$\psi (t)为父小波，\phi (t)为母小波$$

母小波性质：
$$1.平移正交性：<\phi (t),\phi (t-kT)>=0$$

$$2.归一化：<\phi (t),\phi (t)>={\int }_{-\infty }^{\infty }{\phi }^2(t)dt=1$$

父小波性质：
$$1.平移正交性：<\psi (t),\psi (t-kT)>=0$$

$$2.归一化：<\psi (t),\psi (t)>={\int }_{-\infty }^{\infty }{\psi }^2(t)dt=1$$

$$3.与母小波\phi (t)正交$$

• 足够的消失矩m

$${\int }_R{t}^k\phi (t)dt=0,0\le k\le m$$

消失矩阶数的大小反映信号微小突变的检测能量。

• 紧支性

指定义域是有限的范围

小波的紧支区间越小，越容易确定信号的突变点。

• 对称性

在信号分析中，具有线性相位的小波函数可以避免对信号小波分解与重构时的相位失真。

• 正交性

正交基是对信号效率最高的表达方式，但会有Gibbs效应

同一尺度下小波函数与尺度函数内积为零

不同尺度之间的小波函数内积为零

同一尺度下时间轴上任意两个小波函数内积为零

• 正则性

正则性描述小波基函数的平滑程度，正则性随消失矩的增加而加强。

• 小波变换

小波变换只对信号的低频部分做进一步分解，而对高频部分也即信号的细节部分不再继续分解，所以小波变换能够很好地表征一大类以低频信息为主要成分的信号，不能很好地分解和表示包含大量细节信息（细小边缘或纹理）的信号，如非平稳机械振动信号、遥感图象、地震信号和生物医学信号等

• 小波包变换

小波包变换既可以对低频部分信号进行分解，也可以对高频部分进行分解，而且这种分解既无冗余，也无疏漏，所以对包含大量中、高频信息的信号能够进行更好的时频局部化分析。

小波分析的应用领域十分广泛，它包括：数学领域的许多学科；信号分析、图象处理；量子力学、理论物理；军事电子对抗与武器的智能化；计算机分类与识别；音乐与语言的人工合成；医学成像与诊断；地震勘探数据处理；大型机械的故障诊断等方面；例如，在数学方面，它已用于数值分析、构造快速数值方法、曲线曲面构造、微分方程求解、控制论等。在信号分析方面的滤波、去噪声、压缩、传递等。在图象处理方面的图象压缩、分类、识别与诊断，去污等。在医学成像方面的减少B超、CT、核磁共振成像的时间，提高分辨率等。

matlab小波变换程序

clear all;
close all;
load noissin.mat;
figure;
noissin1 = wdenoise(noissin,7, ...
    'Wavelet', 'sym4', ...
    'DenoisingMethod', 'Bayes', ...
    'ThresholdRule', 'Median', ...
    'NoiseEstimate', 'LevelIndependent');%小波分解降噪
subplot(221);

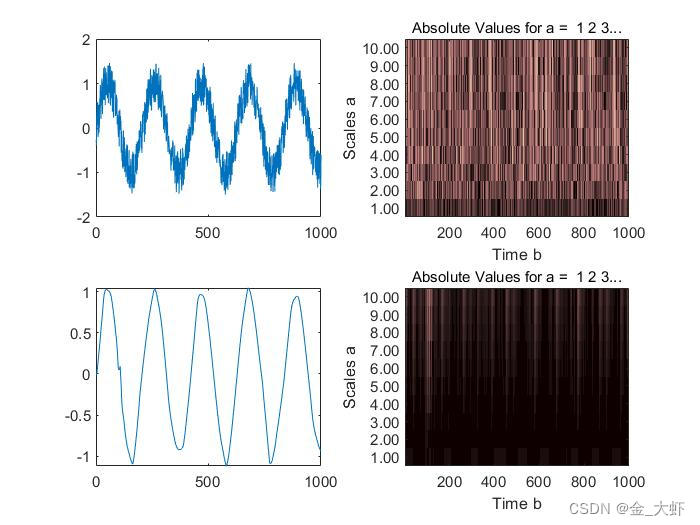
plot(noissin);                        %信号的时域图   1000个点

subplot(222);
%%  noissin是信号，1:10是尺度，db2是小波类型，plot是显示变换后的图形，返回系数
c=cwt(noissin,1:10,'db2','plot');      %  系数图 
subplot(223);
plot(noissin1);
subplot(224);
c=cwt(noissin1,1:10,'db2','plot');      %  系数图 

matlab小波包变换程序