如何获得模型的输入端口？

• 建立电路模型的方法分析如下buck电路由串联电阻电感绕线电阻$R_L$代替
  
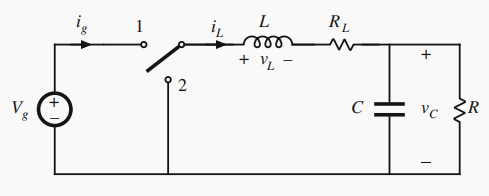
• 电感电压平均值为$$<v_L>=0=D{V}_g?I_L{R}_L-V_C$$
• 这个方程描述了一个具有直流电感电流$I_L$的环路，且环路各个电压有
  • 受控电压源$D{V}_g$
  • 电阻$R_L$上的压降$I_L{R}_L$
  • 输出电压$V_C$
• 电容电流平均值为$$<i_C>=0=I_L-\frac{V}{R}$$
• 这个方程描述了流入电容节点的直流电流。电感直流电流$I_L$流入节点，负载电阻电流$V/R$流出节点。可以求解出直流输出电压$V_C$。
  
• 如上图，根据已知表达式来构建的电路图，现在我们希望在buck变换器的模型中同样包含一个直流变压器，其匝比等于直流变换比，即$1:D$。根据buck原理图可知，变压器的次级等效为一个值为$D{V}_g$的受控电压源，但问题是，变压器的初级在哪里？根据前面所学知识，我们期望初级等效为一个受控电流源。要想找到这个源，我们必须找到变换器的输入电流$i_g(t)$的直流分量。
• 如下图，输入电流$i_g(t)$的波形图
  
• 开关为1位置时，忽略电感纹波电流，即$i_g(t)\approx I_L$；开关为2位置时，$i_g(t)=0$，因此$i_g(t)$的直流分量（或平均值）为$$I_g=\frac{1}{T_s}{\int }_0^{T_s}{i}_g(t)dt=D{T}_s$$
• 因此得到变换器从电源$V_g$输出的电流直流分量$I_g=D{I}_L$，则构建电路如下
  
• 结合初级跟次级电路模型，可得到完整模型
  
• 将其等效为匝比$1:D$的直流变压器
  
• 通常，要获得对变换器输入端口建模的完整直流等效电路，必须为变换器的直流输入电流列写相应的方程，然后构造对应于该方程的等效电路。

实例：boost电路中的半导体器件损耗

• 前面我们聊过boost电路的铜损，但是对于实际电路来说，包含了由半导体构成的mos开关管和续流二极管，它们会产生一定的功率损耗。
• MOSFET或BJT的导通压降可以用导通电阻$R_{on}$建模替代。
• 二极管，IGBT，晶闸管，用电压源加上导通电阻会得到精度较高的模型。如果在单个工作点，可以省略其导通电阻。
  
• 如上图，当栅极驱动信号为高电平时，MOS导通且二极管方向截止，电路简化为
  
• 电感电压和电容电流关系式为：$$v_L(t)=V_g-i{R}_L-i{R}_{on}\approx V_g-I{R}_L-I{R}_{on}$$ $$i_C(t)=-\frac{v}{R}\approx -\frac{V}{R}$$
• 当栅极驱动信号为低电平时，MOS截止，反向二极管导通，电路简化为
  
• 电感电压和电容电流关系式为：$$v_L(t)=V_g-i{R}_L-V_D-i{R}_D-v\approx V_g-I{R}_L-V_D-I{R}_D-V$$ $$i_C(t)=i-\frac{v}{R}\approx I-\frac{V}{R}$$
• 波形如下
  
• 一个周期内，电感电压平均值为 $$<v_L>=D(V_g-I{R}_L-$$
  锐单商城拥有海量元器件数据手册、IC替代型号，打造电子元器件IC百科大全！