CS224N WINTER 2022（三）RNN、语言模型、梯度消失与梯度爆炸（附Assignment3答案）

时间：2023-12-23 15:37:02 j95组合式连接器

CS224N WINTER 2022(1)词向量(附)Assignment1答案）
CS224N WINTER 2022(2)反向传播、神经网络、依存分析(附件)Assignment2答案）
CS224N WINTER 2022（三）RNN、语言模型、梯度消失和梯度爆炸Assignment3答案）
CS224N WINTER 2022年(4)机器翻译注意力机制subword模型（附Assignment4答案）
CS224N WINTER 2022（五）Transformers详解（附Assignment5答案）

序言

CS224N WINTER 2022课件可从https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1224/下载，也可从以下网盘获取:
```
https://pan.baidu.com/s/1LDD1H3X3RS5wYuhpIeJOkA 提取码: hpu3 
```
本系列博客的开头还将提供下载链接，总结相应的课件。
课件、作业答案、学习笔记（Updating）：GitHub@cs224n-winter-2022
本系列博客内容说明：
- 作者根据自己的情况记录更有用的知识点，并提出少量的意见或扩展延伸，而不是slide内容完整笔注；
- CS224N WINTER 2022年共五次作业，作者提供自己完成的参考答案，不保证其正确性；
- 由于CSDN限制博客字数，作者不能在博客中发表完整内容，只能分篇发布，可以从我身上发布GitHub Repository获得完整的笔记，本系列其他分篇博客发布（Updating）：
  
  CS224N WINTER 2022（一）词向量（附Assignment1答案）
  
  CS224N WINTER 2022(2)反向传播、神经网络、依存分析(附件)Assignment2答案）
  
  CS224N WINTER 2022（三）RNN、语言模型、梯度消失和梯度爆炸Assignment3答案）
  
  CS224N WINTER 2022年(4)机器翻译注意力机制subword模型（附Assignment4答案）
  
  CS224N WINTER 2022（五）Transformers详解（附Assignment5答案）

文章目录

序言
- lecture 5 循环神经网络和语言模型
- - slides
  - notes
  - suggested readings
  - assignment3 参考答案
  - - 1. Machine Learning & Neural Networks
    - 2. Neural Transition-Based Dependency Parsing
- lecture 6 梯度消失和爆炸，变体RNN，seq2seq
- - slides
  - notes
  - suggested readings

lecture 5 循环神经网络和语言模型

slides

[slides]

神经依赖分析模型架构：slides p.4

传统的依赖分析方法涉及稀疏和不完整的类别特征，因此需要花费大量的时间进行特征操作；神经网络方法可以学习密集的特征来更好地解决问题。

这里再提一遍lecture3的notes部分提到的greedy Greedy Deterministic Transition-Based Parsing例如，神经网络处于给定状态的三元组 $(\sigma,\beta,A)$ 在特征表示下，预测下一次可能的转移(三种转移策略之一)。

与Neural transition-based对应相应的依存分析模型Neural graph-based依存解析模型，它要预测的就是图节点（单词）之间的依存关系是否存在，有点类似证明图。

### notes

神经依存分析的评价指标：slides p.5

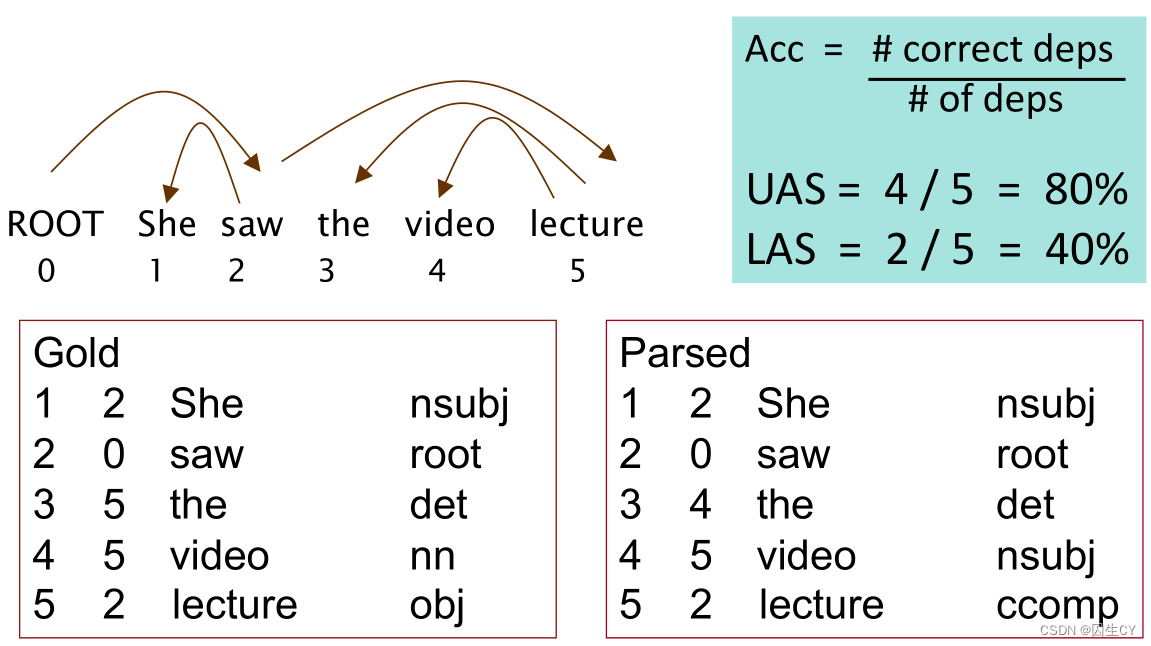
左边的Gold是依赖分析训练集的标记格式，包括对词性标记的预测和对依赖关系的预测。

看起来UAS这取决于关系的准确性，LAS是词性标记的准确性。（这种解释是合理的）

正好看了这部分，又查了另一个博客，感觉比我说得更清楚。

神经网络参数初始化：slides p.16

这个在lecture3的式 $(3.7)$ 中也有提过一次，这里提到的初始化规则是：
- 权重矩阵的数值在 $\text{Uniform}(-r,r)$ 的分布上采样，尽量确保初始值的方差满足下式：
  $\text{Var}(W_i)=\frac2{n_{\rm in}+n_{\rm out}}\tag{5.1}$
  其中 $n_{\rm in}$ 与 $n_{\rm out}$ 分别表示 $W_i$ 的fan-in与fan-out；
语言模型：slides p.19-22

语言模型旨在给定单词序列的条件下，预测下一个单词是什么（输入法的联想）：
$P(x^{(t+1)}|x^{(t)},...,x^{(1)})\tag{5.2}$
也可以看作是计算一段文本出现的概率（文本校正）：
$\begin{aligned} P(x^{(1)},...,x^{(T)})&=P(x^{(1)})\times P(x^{(2)}|x^{(1)})\times...\times P(x^{(T)}|x^{(T-1)},...,x^{(1)})\\ &=\prod_{t=1}^TP(x^{(t)}|x^{(t-1)},...,x^{(1)}) \end{aligned}\tag{5.3}$
n-gram模型：slides p.23-32

最经典的统计语言模型莫过于n-gram模型，即只考虑长度不超过n的单词序列的转移概率与分布概率，假定：
$\begin{aligned} P(x^{(t+1)}|x^{(t)},...,x^{(1)})&=P(x^{(t+1)}|x^{(t)},...,x^{(t-n+2)})\\ &=\frac{P(x^{(t+1)},x^{(t)},...,x^{(t-n+2)})}{P(x^{(t)},...,x^{(t-n+2)})}\\ &\approx\frac{\text{count}(x^{(t+1)},x^{(t)},...,x^{(t-n+2)})}{\text{count}(x^{(t)},...,x^{(t-n+2)})} \end{aligned}\tag{5.4}$

最终可以使用大规模语料库中的统计结果进行近似。

当然这种假定可能并不总是正确，因为文本中的相互关联的单词可能会间隔很远，并不仅能通过前方少数几个单词就能正确推断下一个单词。

总体来说，n-gram模型的存在如下两个显著的缺陷：
- 稀疏性：可能一段文本根本就从来没有出现过；
- 高内存占用：存储文本中所有的n-gram值耗用非常大，因此一般n的取值都很小。这里笔者可以推荐一个公开的英文2-gram与3-gram数据，以arpa格式的文件存储，具体使用可以参考笔者的博客。
神经语言模型与RNN：slides p.33

这种解决与序列预测相关的学习任务，正是RNN大展身手的时候，损失函数使用交叉熵。

由于大多是RNN的基础内容，没有特别值得记录的内容，提醒一下RNN是串行结构，因此无法并行提速。

这里记录slides中几个小demo的项目地址：
- 使用n-gram模型自动生成文本：language-models
- 利用RNN语言模型生成奥巴马讲话：obama-rnn-machine-generated-political-speeches
- 自动智能写作（模仿哈利波特小说风格）：how-to-write-with-artificial-intelligence
语言模型评估指标：slides p.56
- 标准的语言模型评估指标是混乱度（perplexity）：
  $\text{perplexity}=\prod_{t=1}^T\left(\frac1{P_{\rm LM}(x^{(t+1)}|x^{(t)},...,x^{(1)})}\right)^{1/T}\tag{5.5}$
  其实这是关于交叉熵损失函数的指数值：
  $=\sum_{t=1}^T\left(\frac1{\hat y_{x_{t+1}}^{(t)}}\right)^{1/T}=\exp\left(\frac1T\sum_{t=1}^T-\log\hat y_{x_{t+1}}^{(t)}\right)=\exp(J(\theta))\tag{5.6}$

CS224N WINTER 2022（三）RNN、语言模型、梯度消失与梯度爆炸（附Assignment3答案）

文章目录

相关文章