【现代信号处理第六次作业】

时间：2023-12-09 03:07:01 传感器dfs

第六次现代信号处理作业

1. 圆周卷积的定义如下
2. DTFT和DFT变换
3. 小波强制去噪
4. 二次小波图像变换
5. 心得和体会

1. 圆周卷积的定义如下

定义长度为N的有限长序列循环卷积(圆周卷积)
$x_1(n)\otimes x_2(n)=\sum_{i=0}^{N-1}{x_1(i)x_2((n-i)})_N$
循环卷积所得序列的长度还是N，长度不变。
其中表示对进行圆周右移m运算，如长度为6的序列，其图形及圆周移位的图形如下图所示：

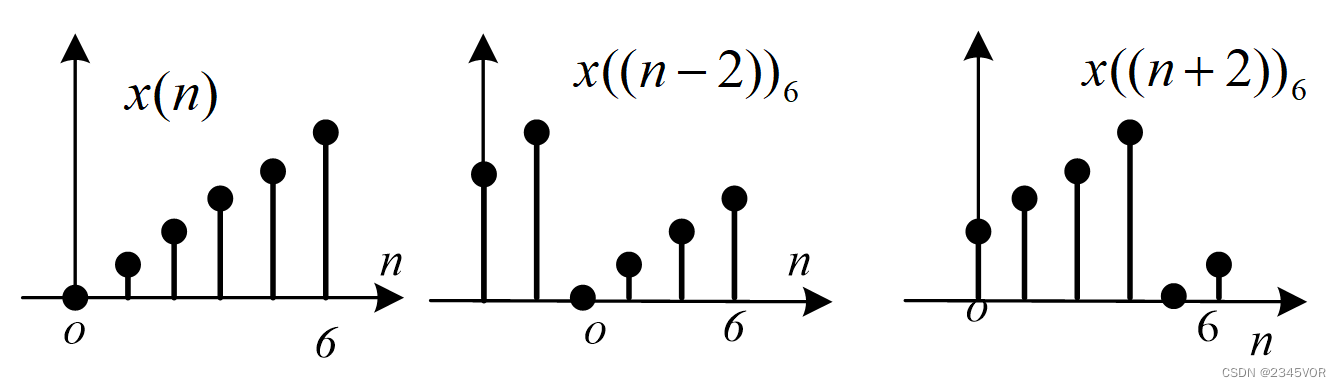
（a）（b）（c）
长度为N的序列通过长度为L（ L $y(n)=x_1(n)\otimes h_1(n)=\sum_{i=0}^{N-1}{x_1(i)h_1((n-i)})_N$
其中是将的长度扩展到N（补零）得到。
如长度为4的有限长序列x(n)={1，1，1，1},通过系统h(n)={n=0,1,2}，则有 $h_1(n)={1， 2，0，0}$ 响应为
$y(0)=x(0)h_1((0))_4+x_1(1)h_1((-1))_4+x_1(2)h_1((-2))_4+x(3)h_1((-3))_3$
$x_1(0)h_1(0)+x_1(1)h_1(3)+x_1(2)h_1(2)+x(3)h_1(1)$
$y(1)=x(0)h_1((1))_4+x_1(1)h_1((0))_4+x_1(2)h_1((-1))_4+x(3)h_1((-2))_3$
$=x_1(0)h_1(1)+x_1(1)h_1(0)+x_1(2)h_1(3)+x(3)h_1(2)\bigm......$
参考我们上课讲到的卷积实现的算法完成下列问题
问题：序列 $x(n)=cos{(}0.2\pi n)$ ，通过系统 $h_1(n)={1， 2，0，0}$ ；
（1）用matlab完成下列圆周卷积的结果（的长度取100）,并与matlab的cconv(x1,x2,N)函数结果进行比较。
（2）比较圆周卷积和线性卷积（conv普通卷积）所得到的结果，分析圆周卷积的优点。（20分）
解：（1）
代码：
定义圆周卷积函数circonvt

function y=circonvt(x1,x2,N) 
x_1=[x1 zeros(1,N-length(x1))]; 
h_1=[x2 zeros(1,N-length(x2))]; 
y1=conv(x_1,h_1);
z_1=[zeros(1,N) y1(1:(N-1))]; 
z_2=[y1((N+1):(2*N-1)) zeros(1,N)];
z=z_1(1:(2*N-1))+z_2(1:(2*N-1))+y1(1:(2*N-1)); 
y=z(10:N+10);
end

%% 1圆周卷积的定义如下
%（1）
clc;clear;
n=20;
t=0:99;
t1=0:n-1;
xn=cos(0.2*pi*t);
hn=[1,-2,2,-1,zeros(1,96)];
y1=circonvt(xn,hn,100);
y2=cconv(xn,hn,100);
hn=hn(1:n);
Y1=y1(1:n);
Y2=y2(1:n);
figure(1);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y1); ylabel ('Y1'); xlabel ('t');title('自定义圆周卷积circonvt'); grid on;
subplot(1,3,3);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
hold on;
%%

如图1：

图1
对比上图可知，两种图像一致，说明函数构造正确。
（2）
代码：

%（2）
y3=conv(xn,hn);
Y3=y3(1:n);
figure(2);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
subplot(1,3,3);
stem(t1,Y3); ylabel ('Y3'); xlabel ('t');title('matlab线性卷积conv'); grid on;
%%

如图2：

图2
对比分析可得，圆周卷积是周期函数，线性卷积不是周期函数，线性卷积后面周期与圆周卷积一致。

2. DTFT和DFT变换

无限长序列，（1）画出其幅度谱；（2）将序列截取长度N=128的有限长序列，画出其DTFT频谱和DFT频谱。（3）例举计算机借助傅里叶变换分析信号频谱的步骤和方法，并指出会带来那些失真？（20分）
解：（1）
代码：
dfs函数

function[Xk]=dfs(xn,N)
n=0:N-1;
k=0:N-1;
WN=exp(-j*2*pi/N)元器件数据手册、IC替代型号，打造电子元器件IC百科大全！

【现代信号处理第六次作业】

第六次现代信号处理作业

相关文章