滤波思维实验-预测值&估计值
时间:2023-09-23 03:37:02
滤波思维实验-预测值&估计值
文章目录
- 滤波思维实验-预测值&估计值
-
- 例如体重秤
- A秤比B秤更精确
- 秤等精度,测量多次
- 加上你的体重增长假设
- 预测&测量的混合
-
- 预测值与测量值的混合比:scale_factor
- 体重变化速率猜测错误(预测值不准确)
- 还需要更新体重增长率(更新增益率)
原地址: (https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python),本文源于其翻译和删除注释的总结
建议下载完整,边看本文边运行下载好的代码
import numpy as np#不需要看代码 #format the book作者定制的包更好地通过图纸展示原理 import book_format import kf_book.gh_internal as gh import kf_book.book_plots as book_plots book_format.set_style() %matplotlib inline 例如体重秤
想象一下,我们生活在一个没有秤的世界里——你站在上面称重。一天,在工作中,一位同事跑过来向你宣布她发明了一个秤。她解释后,你急切地站在上面宣布结果:172磅。你欣喜若狂——这是你有生以来第一次知道自己的体重。更重要的是,当你想象把这个设备卖给世界各地的减肥诊所时,美元符号会在你眼里跳舞!这太棒了!
另一位同事听到了骚动声,来看看是什么让你如此兴奋。你解释了这项发明,再次站在天平上,骄傲地宣布结果:161磅。然后你犹豫了,迷茫了。
几秒钟前读172磅,你向同事抱怨。
我从来没有说过这是准确的,她回答。
传感器不准确。这是大量滤波工作背后的动机。解决这个问题是这本书的主题。我可以提供过去半个世纪发展起来的解决方案,但这些解决方案是通过对我们所知道的东西的性质以及我们如何知道它提出了非常基本的问题而发展起来的。在我们尝试数学之前,让我们跟随这次发现之旅,看看它是否能告诉我们滤波的直觉。
试试另一个秤
我们能做些什么来改进这个结果吗?显然,首先要尝试的是得到一个更好的传感器。不幸的是,你的同事告诉你,她已经做了10个秤,它们的精度几乎是一样的。你让她拿出另一个秤,你称重一个秤,然后称重另一个秤。
-
第一个刻度(A)读数为160磅,第二刻度(B)读数为170磅。 关于你的体重,我们能得出什么结论?我们的选择是什么? * 只相信A,体重为160磅。 * 只相信B,体重为170磅。 * 选择比A和B都是小数字。 * 选择比A和B大数字。 * 在A和B之间选择一个数字。
前两种选择是合理的,但我们没有理由偏爱一种尺度。为什么我们会选择相信A而不是B?我们没有理由相信这一点。第三和第四种选择是不合理的。诚然,这些量表并不十分准确,但根本没有理由选择一个超出两者测量范围的数字。最后的选择是唯一合理的选择。如果两种体重秤都不准确,结果很可能高于我的实际体重,低于我的实际体重,答案通常是a和B之间。
这个概念在数学中被形式化期望值,稍后我们将深入讨论它。现在问问自己,如果读一百万读数,会发生什么通常的事情。有时两个秤的读数太低,有时两个秤的读数太高,剩下的时间会超过实际重量。如果它们跨越实际重量,我们当然应该在A和B之间选择一个数字。如果它们不交叉,我们不知道它们是太高还是太低,但通过A和AB在选择数字之间,我们至少可以减少最差测量的影响。例如,假设我们的实际重量是180磅。160磅是个大错误。但是,如果我们选择160磅到170磅之间的重量,我们的估计值会比160磅好。假如两个天平返回的值大于实际重量,则建立相同的论点。
我们稍后会更正式地处理这个问题,但现在我希望很明显,我们最好的估计是A和B的平均值。
160 170 2 = 165 \frac{160 170}{2} = 165 2160 170=165
我们可以用图形的方式来观察这一点。我已经绘制了A和B的测量值,假设误差为正负8磅。测量值介于160和170之间,因此唯一有意义的重量必须在160和170磅之间。
import kf_book.book_plots as book_plots#这里是作者自定义的一些画图包,不用看这个代码,看图即可
from kf_book.book_plots import plot_errorbars
plot_errorbars([(160, 8, 'A'), (170, 8, 'B')], xlims=(150, 180))
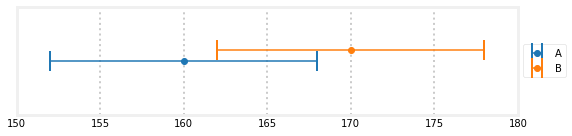
所以165磅看起来是一个合理的估计,但这里有更多的信息,我们可以利用。唯一可能的权重位于A和B的误差条之间的交点处。例如,161磅的重量是不可能的,因为天平B不能给出161磅的读数,最大误差为8磅。同样,169磅的重量是不可能的,因为秤a不能给出169磅的读数,最大误差为8磅。在本例中,唯一可能的重量在162到168磅的范围内。
A秤比B秤更精确
这还不能让我们找到一个更好的体重估计值,但让我们再玩一些“假设”游戏。如果我们现在被告知A比B精确三倍呢?考虑上面列出的5个选项。在A和B范围之外选择一个数字仍然是没有意义的,所以我们不会考虑这些。选择A作为我们的估计值似乎更有说服力——毕竟,我们知道它更准确,为什么不用它代替B呢?B能比A单独提高我们的知识吗?
答案可能与直觉相反,是的,它可以。首先,让我们看看A=160和B=170的相同测量值,但误差为A,3磅,B的误差为A的3倍,9磅。
plot_errorbars([(160, 3, 'A'), (170, 9, 'B')], xlims=(150, 180))
A和B的误差条重叠是唯一可能的真实重量。这种重叠比单独使用时的误差小。更重要的是,,在这种情况下,我们可以看到重叠不包括160磅或165磅。如果我们只使用A的测量值,因为它比B更准确,我们将给出160磅的估计值。如果我们平均A和B,我们将得到165磅。鉴于我们对天平精度的了解,这些权重都不可能。通过包括B的测量,我们将给出介于161 lbs和163 lbs之间的估计值,即两个误差条相交的极限。
让我们把这个限制到极限。假设我们知道秤A精确到1磅。换句话说,如果我们真的重达170磅,它可能报告169磅、170磅或171磅。我们也知道秤B精确到9磅。我们对每个秤进行称重,得到A=160,B=170。我们应该估计我们的重量是多少?让我们以图形的方式来看这一点。
plot_errorbars([(160, 1, 'A'), (170, 9, 'B')], xlims=(150, 180))
在这里我们可以看到,唯一可能的重量是161磅。这是一个重要的结果。使用两个相对不准确的传感器,我们能够推断出极其准确的结果。
因此,两个传感器,即使一个不如另一个准确,也比一个好。
在本书的其余部分,我将反复强调这一点。我们从不丢弃信息,不管它有多差。我们将开发数学和算法,使我们能够包括所有可能的信息来源,以形成可能的最佳估计。
秤是等精度,测许多次
然而,我们已经偏离了我们的问题。没有客户会想购买多个天平,而且,我们最初的假设是,所有天平都是同等准确的。不管精度如何,使用所有测量的洞察力将在以后发挥重要作用,所以不要忘记它。
如果我有一个秤,但我给自己称了很多次呢?我们得出的结论是,如果我们有两个精度相同的量表,我们应该平均它们的测量结果。如果我用一个秤称自己10000倍怎么办?我们已经指出,比额表返回的数字太大的可能性与返回的数字太小的可能性相同。要证明大量权重的平均值将非常接近实际权重并不难,但现在让我们编写一个模拟。
import numpy as np
measurements = np.random.uniform(160, 170, size=1000000)
mean = measurements.mean()
print(f'Average of measurements is {
mean:.4f}')
Average of measurements is 164.9988
打印的确切数字取决于随机数生成器,但它应该非常接近165。
这段代码做出了一个可能不正确的假设——对于165磅的真实重量,秤的读数可能是160或165。这几乎是不正确的。真正的传感器更可能获得更接近真实值的读数,并且越来越不可能获得离真实值越远的读数。我们将在高斯一章中详细介绍这一点。现在,我将使用“numpy”而不作进一步解释。随机的normal()`函数,它将在165磅附近产生更多的值,而在更远的地方产生更少的值。相信现在,这将产生类似于真实天平工作原理的噪音测量。
mean = np.random.normal(165, 5, size=1000000).mean()
print(f'Average of measurements is {
mean:.4f}')
Average of measurements is 164.9920
答案同样非常接近165。
好的,很好,我们找到了传感器问题的答案!但这不是一个非常实际的答案。没有人有耐心称自己一万倍,甚至十几倍。
加上自己的体重增速“假设”
那么,让我们玩“假设”吧。如果你每天测量一次体重,然后得到170、161、169的读数,你的体重是增加了,还是减轻了,或者这些都只是噪音测量?
我们真的不能说。第一次测量是170,最后一次是169,这意味着损失了1磅。但如果刻度仅精确到10磅,这可以用噪音来解释。我本来可以增加体重的;也许第一天我的体重是165磅,第三天是172磅。有可能在体重增加的情况下得到这些体重读数。我的体重秤告诉我我正在减肥,而我实际上正在增重!让我们看一张图表。我已经绘制了测量值和误差条,然后是一些可能的体重增加/减少,这些可以用绿色虚线来解释。
import kf_book.gh_internal as gh
gh.plot_hypothesis1()
正如我们看到的,有一个极端的重量变化范围,可以用这三个测量值来解释。事实上,有无数的选择。我们放弃好吗?不是我!回想一下,我们谈论的是测量人的体重。对于一个人来说,没有合理的方法可以在第一天体重180磅,第三天体重160磅。或者在一天内减掉30磅,但在第二天又恢复了体重(我们假设此人没有发生截肢或其他创伤)。
我们正在测量的物理系统的行为应该影响我们如何解释测量。如果我们每天称量一块石头(很难有重量变动),我们会把所有的差异归因于噪音。如果我们称的是一个由雨水供应并用于家务的蓄水池(受天气影响大),我们可能会认为这种重量变化是真实的。
假设我用一个不同的尺度,我得到以下测量值:169,170,169,171,170,171,169,170,169,170。你的直觉告诉你什么?例如,你可能每天增加1磅,而嘈杂的测量结果恰好让你保持了同样的体重。同样,你可以每天减掉1磅,得到同样的读数。但这有可能吗?掷硬币连续得到10个人头的可能性有多大?不太可能。我们不能仅仅根据这些数据来证明这一点,但我的体重很可能保持稳定。在下面的图表中,我用误差条绘制了测量值,并用绿色虚线标出了可能的真实重量。这条虚线并不是这个问题的“正确”答案,只是一条合理的答案,可以通过测量来解释。
gh.plot_hypothesis2()
另一个假设:如果读数是158.0, 164.2, 160.3, 159.9, 162.1, 164.6, 169.6, 167.4, 166.4, 171.0呢?让我们看一张图表,然后回答一些问题。
gh.plot_hypothesis3()
我的体重“似乎”减轻了,而这只是一个非常嘈杂的数据吗?不是真的。我的体重似乎也一样吗?同样,没有。随着时间的推移,这些数据呈上升趋势;不是均匀的,但肯定是向上的。我们不能确定,但这看起来像是体重增加,而且是一个显著的体重增加。让我们用更多的图来检验这个假设。与表格相比,在图表中“观察”数据通常更容易。
让我们来看两个假设。首先,假设我们的体重没有变化。为了得到这个数字,我们同意我们应该平均测量值。让我们看看这个。
gh.plot_hypothesis4()
这看起来不太令人信服。事实上,我们可以看到,在所有的误差条内没有我们可以画的水平线。
现在,让我们假设我们体重增加了。多少?我不知道,但是NumPy知道!我们想通过测量画一条线,看起来“大约”正确。NumPy的函数将根据称为“最小二乘拟合”的规则执行此操作。让我们不用担心计算的细节,只需绘制结果。
gh.plot_hypothesis5()
至少在我看来,这看起来好多了。请注意,现在假设非常接近每个测量值,而在前面的图中,假设通常离测量值非常远。我体重增加似乎比没有增加更可能是真的。我真的增加了13磅吗?谁能说呢?这似乎不可能回答。
“但这是不可能的吗?”一位同事抱怨道。
让我们试试疯狂的东西。让我们假设我知道我每天大约增加一磅。不管我现在怎么知道,假设我知道它大致正确。也许我每天的饮食是6000卡路里,这会导致体重增加。或者也许有另一种方法来估计体重增加。这是一个思想实验,细节并不重要。让我们看看如果这些信息可用,我们是否可以利用它们。
第一次测量是158。我们无法知道有什么不同,所以让我们接受这一估计。如果我们今天的体重是158,明天会是多少?嗯,我们认为我们的体重每天增加1磅,所以我们的预测是159磅,就像这样:
gh.plot_estimate_chart_1()
好吧,但这有什么用?当然,我们可以假设1磅/天是准确的,并预测我们未来10天的体重,但如果我们不合并读数,为什么还要使用磅秤呢?让我们来看下一个测量。我们再次踏上天平,它显示出164.2磅。
gh.plot_estimate_chart_2()
我们有个问题。我们的预测与我们的测量不符。但是,这正是我们所期望的,对吗?如果预测值始终与测量值完全相同,则无法向过滤器添加任何信息。当然,也没有理由去衡量,因为我们的预测是完美的。
预测&测量的混合
整本书的关键观点在下一段。仔细阅读!
那我们该怎么办?如果我们仅根据测量结果进行估计,那么预测将不会影响结果。如果我们仅从预测中形成估计,那么测量将被忽略。若要做到这一点,我们需要**采取某种预测和测量的混合方式**(我将关键点用黑体标出)。
混合两个值-这听起来很像前面的双尺度问题。使用与之前相同的推理,我们可以看到唯一有意义的事情是在预测和测量之间选择一个数字。例如,165的估计值没有意义,157也没有意义。我们的估计值应该在159(预测值)和164.2(测量值)之间。
再说一次,这很重要。我们一致认为,当呈现两个有误差的值时,我们应该在两个值之间形成一个估计值。这些值是如何生成的并不重要。在本章开始时,我们有两个测量值,但现在我们有一个测量值和一个预测值。在这两种情况下,推理和数学都是一样的。我们从不丢弃信息。我是认真的。我看到很多商业软件扔掉了嘈杂的数据。别这样!我们对体重增加的预测可能不是很准确,但只要有一些信息,我们就应该使用它。
我要你停下来好好想想。我所做的就是用基于人体生理学的不准确的体重预测来代替不准确的体重秤。它仍然是数据。数学不知道数据是来自量表还是预测。我们有两段带有一定数量噪声的数据,我们想要将它们组合起来。在本书的其余部分中,我们将开发一些相当复杂的数学来执行此计算,但数学从不关心数据来自何处,它只根据这些值的值和准确性进行计算。
估计值是否应该介于测量值和预测值之间?也许吧,但总的来说,我们似乎知道我们的预测与测量结果相比或多或少是准确的。我们预测的准确度可能与量表的准确度不同。回想一下,当量表A比量表B准确得多时,我们做了什么——我们将答案量表A比B更接近。让我们看一张图表
gh.plot_estimate_chart_3()
预测值与测量值的混合比例:scale_factor
现在,让我们尝试一个随机选择的数字来缩放我们的估计值:4/10。我们的估计将是测量值的十分之四,其余的将来自预测。换句话说,我们在这里表达了一种信念,一种预测比测量更可能正确的信念。我们将其计算为
e s t i m a t e = p r e d i c t i o n + 4 10 ( m e a s u r e m e n t − p r e d i c t i o n ) \mathtt{estimate} = \mathtt{prediction} + \frac{4}{10}(\mathtt{measurement} - \mathtt{prediction}) estimate=prediction+104(measurement−prediction)
测量和预测之间的差异称为残差,在上图中用黑色垂直线表示。这将成为以后使用的一个重要值,因为它是测量值和滤波器输出之间差异的精确计算。较小的残差意味着更好的性能。
让我们编写代码,并在根据上面的一系列权重进行测试时查看结果。我们必须考虑另一个因素。体重增加以磅/时间为单位,因此为了通用,我们需要添加一个时间步长t,我们将其设置为1(天)。
我手工生成的体重数据对应于160磅的真实起始体重和每天1磅的体重增加。换句话说,第一天(零日)的真实重量为160磅,第二天(第一天,称重的第一天)的真实重量为161磅,依此类推。
我们需要猜测一下初始重量。现在谈论初始化策略还为时过早,所以现在我将假设为160磅。
from kf_book.book_plots import figsize
import matplotlib.pyplot as plt
#weight是几次的测量值
weights = [158.0, 164.2, 160.3, 159.9, 162.1, 164.6,
169.6, 167.4, 166.4, 171.0, 171.2, 172.6]
time_step = 1.0 # 一个时间步为一天
scale_factor = 4.0/10#混合比例
def predict_using_gain_guess(estimated_weight, gain_rate, do_print=False):
# storage for the filtered results
estimates, predictions = [estimated_weight], []
# most filter literature uses 'z' for measurements
for z in weights:
# predict new position
predicted_weight = estimated_weight + gain_rate * time_step
# update filter
estimated_weight = predicted_weight + scale_factor * (z - predicted_weight)
# save and log
estimates.append(estimated_weight)
predictions.append(predicted_weight)
if do_print:
gh.print_results(estimates, predicted_weight, estimated_weight)
return estimates, predictions
initial_estimate = 160.#初始量设定
estimates, predictions = predict_using_gain_guess(
estimated_weight=initial_estimate, gain_rate=1, do_print=True)
previous estimate: 160.00, prediction: 161.00, estimate 159.80
previous estimate: 159.80, prediction: 160.80, estimate 162.16
previous estimate: 162.16, prediction: 163.16, estimate 162.02
previous estimate: 162.02, prediction: 163.02, estimate 161.77
previous estimate: 161.77, prediction: 162.77, estimate 162.50
previous estimate: 162.50, prediction: 163.50, estimate 163.94
previous estimate: 163.94, prediction: 164.94, estimate 166.80
previous estimate: 166.80, prediction: 167.80, estimate 167.64
previous estimate: 167.64, prediction: 168.64, estimate 167.75
previous estimate: 167.75, prediction: 168.75, estimate 169.65
previous estimate: 169.65, prediction: 170.65, estimate 170.87
previous estimate: 170.87, prediction: 171.87, estimate 172.16
# plot results
book_plots.set_figsize(10)
gh.plot_gh_results(weights, estimates, predictions, [160, 172])
weights
[158.0,164.2,160.3,159.9,162.1,164.6,169.6,167.4,166.4,171.0,171.2,172.6]
那太好了!这里有很多数据,所以让我们来谈谈如何解释它。粗蓝线显示来自过滤器的估计值。它从第0天开始,初始猜测为160磅。红线显示根据前一天的体重做出的预测。因此,第一天之前的体重为160磅,体重增加为1磅,因此第一次预测为161磅。第一天的估计值介于预测值和测量值之间,为159.8磅。图表下方是之前体重、预测体重和每天新估计值的打印件。最后,细黑线显示被称重者的实际体重增加。
每天都要做一次这样的练习,确保你了解预测和估计是如何在每一步中形成的。请注意,估计值总是介于测量值和预测值之间。
估计值不是一条直线,但它们比测量值更直,并且有点接近我们创建的趋势线。而且,随着时间的推移,情况似乎有所好转。
过滤器的结果可能会让你觉得很傻;当然,如果我们假设我们的体重增加约为1磅/天,数据看起来会很好!
体重变化速率猜测错误(预测值不准)
如果我们最初的猜测是错误的,过滤器会做什么。让我们预测一下,每天体重会减少1磅:
e, p = predict_using_gain_guess(initial_estimate, -1.)
gh.plot_gh_results(weights, e, p, [160, 172])
估计值很快就偏离了测量值。显然,要求我们正确猜测变化率的过滤器不是很有用。即使我们最初的猜测是正确的,一旦变化率发生变化,过滤器也会失败。如果我不再暴饮暴食,过滤器将很难适应这种变化。请注意,它正在调整!尽管我们告诉它我们每天要减掉1磅,但估计仍在上升。它就是调整得不够快。
体重增速也需更新(更新增益率)
但是,“如果”呢?如果我们不把体重增加留在最初猜测的1磅(或任何东西),而是根据现有的测量和估计来计算增加速率呢。在第一天,我们对重量的估计是:
( 160 + 1 ) + 4 10 ( 158 − 161 ) = 159.8 (160 + 1) + \frac{4}{10}(158-161) = 159.8 (160+1)+104(158−161)=159.8
第二天,我们测量了164.2磅,这意味着体重增加了4.4磅(因为164.2-159.8=4.4磅),而不是1磅。我们能以某种方式利用这些信息吗?这似乎是有道理的。毕竟,体重测量本身是基于对我们体重的真实测量,因此有有用的信息。我们对体重增加的估计可能并不完美,但肯定比仅仅猜测体重增加1磅要好。数据比猜测要好,即使它很嘈杂。
在这一点上,人们真的会犹豫,所以要确保你的意见一致。两次嘈杂的体重测量给了我们一个暗示的体重增加/减少。如果测量值不准确,那么估计值将非常不准确,但计算中仍然有信息。想象一下,用一个精确到1磅的秤称量一头奶牛,它显示奶牛增加了10磅。奶牛可能增加了8磅到12磅,这取决于误差,但我们知道它增加了重量,大约增加了多少。这是信息。我们如何处理信息?永远不要把它扔掉!
回到我的饮食。我们是否应该将新的每日增重设置为4.4磅?昨天我们认为体重增加了1磅,今天我们认为是4.4磅。我们有两个数字,想把它们结合起来。嗯,听起来我们又遇到了同样的问题。让我们使用相同的工具,也是迄今为止唯一的工具——在两者之间选择一个值。这次我将使用另一个任意选择的数字1/3。该方程式与重量估算的方程式相同,但我们必须纳入时间,因为这是一个速率(增重/天):
new gain = old gain + 1 3 measurement - predicted weight 1 day \text{new gain} = \text{old gain} + \frac{1}{3}\frac{\text{measurement - predicted weight}}{1 \text{ day}} new gain=old gain+311 daymeasurement - predicted weight
weight = 160. # initial guess
gain_rate = -1.0 # initial guess增速初始化,也叫增益率
time_step = 1.
weight_scale = 4./10#测量值和预测值的混合比例
gain_scale = 1./3#计算新增速时,旧增速和(测量值-预测值)的比例
estimates = [weight]
predictions = []
for z in weights:#weights里面是测量值
# prediction step
weight = weight + gain_rate*time_step#体重预测值计算
gain_rate = gain_rate
predictions.append(weight)
# update step
residual = z - weight#残差计算
gain_rate = gain_rate + gain_scale * (residual/time_step)#更新增益率
weight = weight + weight_scale * residual
#计算估计值,用估计值代替预测值成为weight,用到下一步预测更新中作为当前步的weight
estimates.append(weight)
gh.plot_gh_results(weights, estimates, predictions, [160, 172])
我认为这看起来真的很好。由于最初猜测体重增加为-1,过滤器需要几天才能准确预测体重,但一旦预测到,它就会开始准确跟踪体重。我们没有使用任何方法来选择4/10和1/3的比例因子(实际上,对于这个问题来说,它们是糟糕的选择),但除此之外,所有的数学都遵循非常合理的假设。在预测步骤中,您需要**预测所有变量的下一个值,包括“权重”和“增益率”**。



