本文涉及的方案：

• MSP：一种Multi-Signature(基于双线性对)合成多个签名，使用合成公钥$apk$可验证。（用全部的$ap{k}_i$一组可以批量验证multi-Signatures）
• AMSP：MSP聚合版，多个multi-Signatures聚合成一个，并给出相应的验证方法
• ASM：部分子集的multi-signature，使用总合成公钥apk可验证，使用$m{k}_i$可追责
• MSDL：基于离散对数Multi-Signature方案

以上方案PoP版本（用PoP对抗 Rogue public-key attack）

• $\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}:(\mathrm{P}\mathrm{g},\mathrm{K}\mathrm{g},\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{n},\mathrm{K}\mathrm{A}\mathrm{g},\mathrm{V}\mathrm{f})$：签名算法的输入包括公钥集合$\mathcal{P}\mathcal{K}$，每个签名方各自生成签名。$\mathrm{K}\mathrm{A}\mathrm{g}$将公钥集合聚合成一个聚合公钥，可用于验证任何一个签名。
• Aggregate Multi-Signatures：将多个Multisignature聚合成一个签名，扩展两个算法：
  • $\mathrm{S}\mathrm{A}\mathrm{g}((apk,m,\sigma ),...)\to \Sigma$
  • $\mathrm{A}\mathrm{V}\mathrm{f}((apk,m),...,\Sigma )\to 0/1$

构造Aggregate Multi-Signatures的目标并非简单的聚合，而是构造远小于独立Multi-Signatures集合的规模，理想状态下是常数规模。

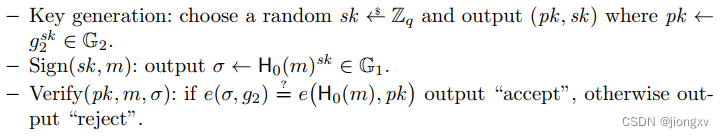
这个签名支持简单的聚合：

验证聚合签名：所有$(p{k}_i,m_i{)}_{i=1}^n$

如果所有被签名的message都一样：$m_1=...=m_n$，验证关系(2)归约成简单的形式：

以及一个短的聚合公钥$apk:=p{k}_1...p{k}_n\in {\mathbb{G}}_2$

• $\mathrm{K}\mathrm{e}\mathrm{y}\mathrm{G}\mathrm{e}\mathrm{n}():x\leftarrow {\mathbb{Z}}_p,X=g^x$
• S i g n ( ( s k , p k ) , L = { p k 1 , . . . , p k n } , m ) → σ {\rm Sign}( (sk, pk),L=\{pk_1,...,pk_n\},m)\rightarrow \sigma Sign((sk,pk),L={ pk1​,...,pkn​},m)→σ. L = { X 1 , . . . , X n } L=\{X_1,...,X_n\} L={ X1​,...,Xn​}，签名者密钥$(x_1,X_1)$

1. 对 i ∈ { 1 , . . . , n } i\in\{1,...,n\} i∈{ 1,...,n}，计算$a_i=H_0(L,X_i)$，聚合公钥$\tilde{X}={\prod }_{i=1}^n{X}_i^{a_i}$
2. 随机$r_i\leftarrow {\mathbb{Z}}_p$，计算$R_1=g^{r_1}$，将$R_1$发送给其他参与方
3. 收到其他所有$R_2,...,R_n$后，计算：$R={\prod }_{i=1}^n{R}_i,c=H_1(\tilde{X},R,m),s_1=r_1+c\cdot a_1\cdot x_{1}modp$，将$s_1$发送给其他参与方
4. 收到所有其他$s_2,...,s_n$后，计算：$s={\sum }_{i=1}^n{s}_{i}modp$，签名$\sigma =(R,s)$

• $\mathrm{V}\mathrm{e}\mathrm{r}(L,m,\sigma )\to 0/1$