动态系统的建模与分析
时间:2023-02-07 08:00:01
参考:DR_CAN
同一领域的文章:
- 建模和分析动态系统
- 自动控制原理
- Advanced控制理论
- 傅里叶级数及变换
- 工程数学
文章目录
-
- 1.介绍
- 2.电路系统建模
- 3.流体系统建模
- 4.拉普拉斯变换
- 5.拉普拉斯变换的收敛域(ROC)与逆变换(ILT)
- 6.拉&传&微的关系
- 7.单位阶跃响应一级系统
- 8.频率响应和滤波器
- 9.一阶系统的频率响应
- 10.二级系统对初始条件的动态响应
- 11.二级系统的单位阶跃响应
- 12.二级系统的性能分析与比较
- 13.二级系统频率响应分析
- 14.伯德图
1.介绍
解决控制系统问题:
- 分析研究对象
- 控制器设计
- 测试
??分析被控对象的物理特性和动态性能,在此基础上建立数学模型。数学模型可以是动力学模型、热力学模型、流体力学模型和经济学模型,然后在数学模型的基础上设计控制器。为了满足不同的要求,应使用不同的控制方法(传统的控制控制,PID然后选择测试平台进行控制、非线性控制、自适应控制和优化控制,可以是仿真平台、实验室模型样机和真实设备等。最后,将实验结果与模型进行比较,不断验证和更新数学模型。
内容:
动态系统建模:
- 电力,KCL,KVL
- 流体
- 热力学
- 机械系统
拉普拉斯 微分方程
时域分析
频域分析
2.电路系统建模
基础元件:
| 基础元件 | 单位 | 符号 |
|---|---|---|
| 电量 | 库仑(c) | q q q |
| 电流 | 安培(A) | i i i |
| 电压 | 伏特(V) | e e e |
| 电阻 | 欧姆(Ω) | R R R |
| 电容 | 法拉(F) | C C C |
| 电感 | 亨利(H) | L L L |
流速: i = d q d t i=\frac{dq}{dt} i=dtdq
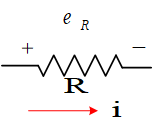
电阻电压: e R = i R e_R=iR eR=iR
电量: q = C e c q=Ce_c q=Cec
e c = 1 C q = 1 C ∫ 0 t i d t e_c=\frac{1}{C}q=\frac{1}{C}\int_0^tidt ec=C1q=C1∫0tidt
电感:
e L = L d i d t = L i ′ e_L=L\frac{di}{dt}=Li^{\prime} eL=Ldtdi=Li′
基尔霍夫定律
KCL:所有进入某节点的电流的总和等于所有离开这个节点的电流的总和。
i 1 + i 2 − i 3 − i 4 = 0 i_1+i_2-i_3-i_4=0 i1+i2−i3−i4=0
KVL:沿着闭合回路所有元件两端的电压的代数和为零。
e R − e = 0 e_R-e=0 eR−e=0
KVL:
e L + e C + e R − e = 0 e_L+e_C+e_R-e=0 eL+eC+eR−e=0
L i ′ + 1 C ∫ 0 t i d t + i R = e Li^{\prime}+\frac{1}{C}\int_0^tidt+iR=e Li′+C1∫0tidt+iR=e
两边求导:
L i ′ ′ + i ′ R + 1 C i = e ′ Li^{\prime\prime}+i^{\prime}R+\frac{1}{C}i=e^{\prime} Li′′+i′R+C1i=e′
L = 2 H C = 1 4 F R 1 = 1 Ω R 2 = 3 Ω L=2H \\C=\frac{1}{4}F\\ R_1=1\Omega\\ R_2=3\Omega L=2HC=41FR1=1ΩR2=3Ω
loop 1:
e L + e C − e i = 0 e_L+e_C-e_i=0 eL+eC−ei=0
loop 2:
e R 1 + e R 2 − e C = 0 e_{R1}+e_{R2}-e_C=0 eR1+eR2−eC=0
合并:
e L + e R 1 + e R 2 − e i = 0 e_L+e_{R1}+e_{R2}-e_i=0 eL+eR1+eR2−ei=0
这是一个大圈,因此在用KVL时,不一定都用小圈,也可用大圈。
e L = L i 1 ′ = 2 i 1 ′ e_L=Li_1^{\prime}=2i_1^{\prime} eL=Li1′=2i1′
e C = 1 C ∫ 0 t ( i 1 − i 2 ) d t = 4 ∫ 0 t ( i 1 − i 2 ) d t e_C=\frac{1}{C}\int_0^t (i_1-i_2) dt=4\int_0^t (i_1-i_2) dt eC=C1∫0t(i1−i2)dt=4∫0t(i1−i2)dt
e R 1 = i 2 R 1 = i 2 e_{R1}=i_2R_1=i_2 eR1=i2R1=i2
e R 1 = i 2 R 2 = 3 i 2 e_{R1}=i_2R_2=3i_2 eR1=i2R2=3i2
loop 1:
2 L i 1 ′ + 4 ∫ 0 t ( i 1 − i 2 ) d t − e i = 0 (1) 2Li_1^{\prime}+4\int_0^t (i_1-i_2) dt-e_i=0\tag{1} 2Li<



