电路-并联谐振电路分析

并联谐振电路

• 为什么要并联谐振电路？根据质量因数章节的研究，串联谐振电路的质量因数与内阻r成反比，r质量因数越大，质量因数越小。如果电源内阻相对较大，我们想要一个高质量因数的谐振电路怎么办？并联谐振电路可用于此时。

GCL并联谐振电路

概念

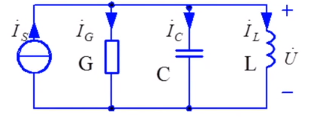
并联GCL电路与rLC串联电路是对偶电路。

• 并联电路总导纳为：$$Y=Gj(wC?\frac{1}{wL})=GjB$$
• 调整激励频率，使电纳B=0，当电纳为0时：$$B=wC?\frac{1}{wL}=0$$
• 并联电路两端电压与激励同相，称发生并联谐振。

电路参数

• 谐振频率：$$w_0=\frac{1}{\sqrt{LC}}(rad/s)或f_0=\frac{1}{2\pi \sqrt{LC}}(Hz)$$
• 特性阻抗：$$\rho =w_{0}L=\frac{1}{w_{0}C}=\sqrt{\frac{L}{C}}(\Omega )$$
• 品质因数（电容器）：$$Q=2\pi \frac{C{U}^2}{U^{2}GT}=\frac{w_{0}C}{G}=w_{0}CR=\frac{R}{w_{0}L}$$

并联谐振电路的特点

• 谐振时，总导纳的模值最小 $$Y=G+j{B}_0=G+j(w_{0}C-\frac{1}{w_{0}L})=G=\frac{1}{R}$$
• 谐振时，端电压模值最大 $$\dot{U}=\frac{\dot{I_s}}{Y_0}=R\dot{I_s}$$
• 流过电导的电流 = 电流源电流 $$\dot{I_{G0}}=G\dot{U}=G\frac{1}{G}\dot{I}=\dot{I_s}$$
• 电容电流是电流源电流Is的Q倍 $$\dot{I_{C0}}=j{w}_{0}C\dot{U}=j\frac{w_{0}C}{G}\dot{I_s}=jQ\dot{I_s}$$
• 电感电流也是电流源电流Is的Q倍，且与电容电流相位相反 $$\dot{I_{L0}}=-j\frac{1}{w_{0}L}\dot{U}=-j\frac{R}{w_{0}L}\dot{I_s}=-jQ\dot{I_s}$$

频率响应

• 如图，以电感上电压为输出，网络函数为 $$H(jw)=\frac{\dot{U}}{\dot{I_s}}$$
• 它是一个带通滤波器，通频带为 B = w 0 Q = G C = 1 R C ( r a d / s ) B=\frac{w_{0}}{Q}=\frac{G}{C}=\frac{1}{RC}(rad/s) 元器件数据手册、IC替代型号，打造电子元器件IC百科大全！