电容ESR与高频零点对buck电路的影响

时间：2022-08-28 09:30:00 输出电容esr 电容的等效串联电阻对电路的影响电容器的等效串联电阻esr f高频电容电容器esr值

以前在网上看一些关于一些关于网上的关于buck在电路和控制器设计的视频中，发现高频相位为-90°理想模型的高频相位为-180°(只有两个极点)。仔细对比表达式，发现主要原因是他们使用的模型添加到输出侧LC滤波电路中的电容器ESR。

电容ESR

电容等效串联电阻（Equivalent series resistance, ESR）与介质层材料、包装、容量、运行频率、工作温度等有关。

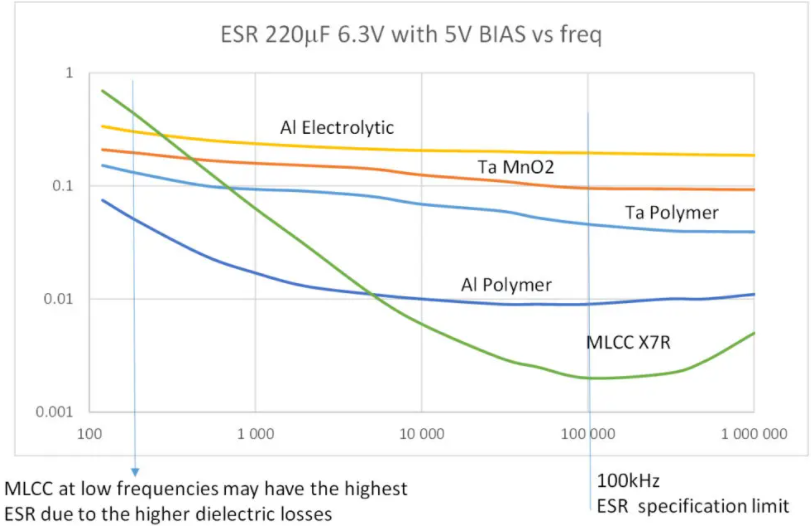
ESR与电容的阻抗都与频率相关，如下图。

ESR和高频零点

不考虑ESR的情况，buck从电路控制到输出的小信号模型为：
$G_c(s)=\frac{V_{in}}{LCs^2 \frac{L}{R}s 1}$
只有有两个极点。

如果考虑ESR rc，控制到输出的小信号模型变为：
$G_c(s)=\frac{V_{in}(r_cCs+1)}{LC(1+\frac{r_c}{R})s^2+(\frac{L}{R}+r_cC)s+1}$
可以看到rc对极点的影响较小，但是新引入一个零点，位于 $f_z=\frac{1}{2\pi r_cC}$ 。

两种模型的波特图对比如下：可见rc主要影响了高频的相位和Q值。

仿真验证

ESR引入的高频零点带来了相位提升，有利于提升相位裕量，使系统更容易保持稳定。当然高ESR会导致更高的纹波和损耗。

有些年代久远的LDO、DC-DC会要求输出侧电容的ESR不小于特定值。同样，也有一些新的产品会标注“不依赖外接电容ESR也能稳定运行”。

举一个较为极端的情况进行简单验证。同一个Buck电路，使用同一套PI参数，设计穿越频率在50kHz（开关频率500kHz），环路增益对比如下：

加入0.1Ω ESR，相位裕量约39°。
不考虑ESR，相位裕量0.5°。

对比两种情况下半载和满载跳变的响应。首先是无ESR的情况，可以看到在满载时，已经出现了较大幅度的振荡。

而对于0.1Ω ESR的情况，输出电压响应很快，并且没有出现振荡。

对于0.1Ω ESR的情况，基于仿真模型测量环路增益的波特图，穿越频率51.8kHz，相位裕量31°，略低于设计值，但也还可以接受。

资料

记录下使用的参数便于后续参考。

主电路与PI控制器参数

传递函数推导

波特图

close all
L=4.7e-6;
C = 22e-6;
Resr = 0.1;
Vi = 12;
Vo = 5;
D = Vo/Vi;
Io = 2;
R = Vo/Io;
Kpwm=1/5;
H = 10/(56+10);


Kp = 3.57;
f_pi = 10e3;
Ki = 2*pi*f_pi;
Gc_pi = tf([Kp, Ki],[1,0]);  %PI
figure(3)
bode(Gc_pi)
R1 = 56e3;
R2 = R1 * Kp;
C1 = 1/(2*pi*R1*f_pi);

f_start = 1e3;
f_end = 100e3;

Gvd = tf(Vi,[L*C,L/R,1]);%buck控制到输出的传递函数 
Gvd_esr = tf(Vi*[C*Resr,1],[L*C*(1+Resr/R),L/R+Resr*C,1]);  %考虑电容Esr，高频的相位改善
figure(1)
compare_bode(Gvd,Gvd_esr,f_start,f_end)

G_open = Kpwm * Gc_pi * tf(Vi,[L*C,L/R,1]);
G_open_esr = Kpwm * Gc_pi * tf(Vi*[C*Resr,1],[L*C*(1+Resr/R),L/R+Resr*C,1]);  %环路增益
figure(2)
compare_bode(G_open,G_open_esr,f_start,f_end)

function compare_bode(Gvd,Gvd_esr,f_start,f_end)
[mag0,ph0,wout] = bode(Gvd,{2*pi*f_start,2*pi*f_end});
[mag_esr,ph_esr,wout_esr] = bode(Gvd_esr,{2*pi*f_start,2*pi*f_end});
fout = wout/(2*pi);
fout_esr = wout_esr/(2*pi);
subplot(2,1,1)
plot(  fout,20*log10(squeeze(mag0(1,1,:))),fout_esr,20*log10(squeeze(mag_esr(1,1,:)))  )
grid;
title('幅频特性')
set(gca, 'XScale', 'log')
% xticks([5e3,15e3,25e3,50e3])
xlabel('Frequency/Hz')
ylabel('Amplitude/dB')
legend('理想','考虑ESR')

subplot(2,1,2)
plot(fout,squeeze(ph0(1,1,:)),fout_esr,squeeze(ph_esr(1,1,:)))
grid;
title('相频特性')
set(gca, 'XScale', 'log')
% xticks([5e3,15e3,25e3,50e3])
xlabel('Frequency/Hz')
ylabel('Phase/\circ')
legend('理想','考虑ESR')

end

参考资料：

Understanding the Impact of ESR on Ceramic Capacitor Selection (knowlescapacitors.com)

SimSurfing (murata.co.jp)

Why Low ESR Matters in Capacitor Design (passive-components.eu)

ESR, Stability, and the LDO Regulator (Rev. A) (ti.com)

锐单商城拥有海量元器件数据手册、IC替代型号，打造电子元器件IC百科大全！

电容ESR与高频零点对buck电路的影响

相关文章